Math
Welcome to the Math Department!
The Fallbrook High School mathematics program strives to challenge, engage, and empower all learners to be lifelong mathematical thinkers.
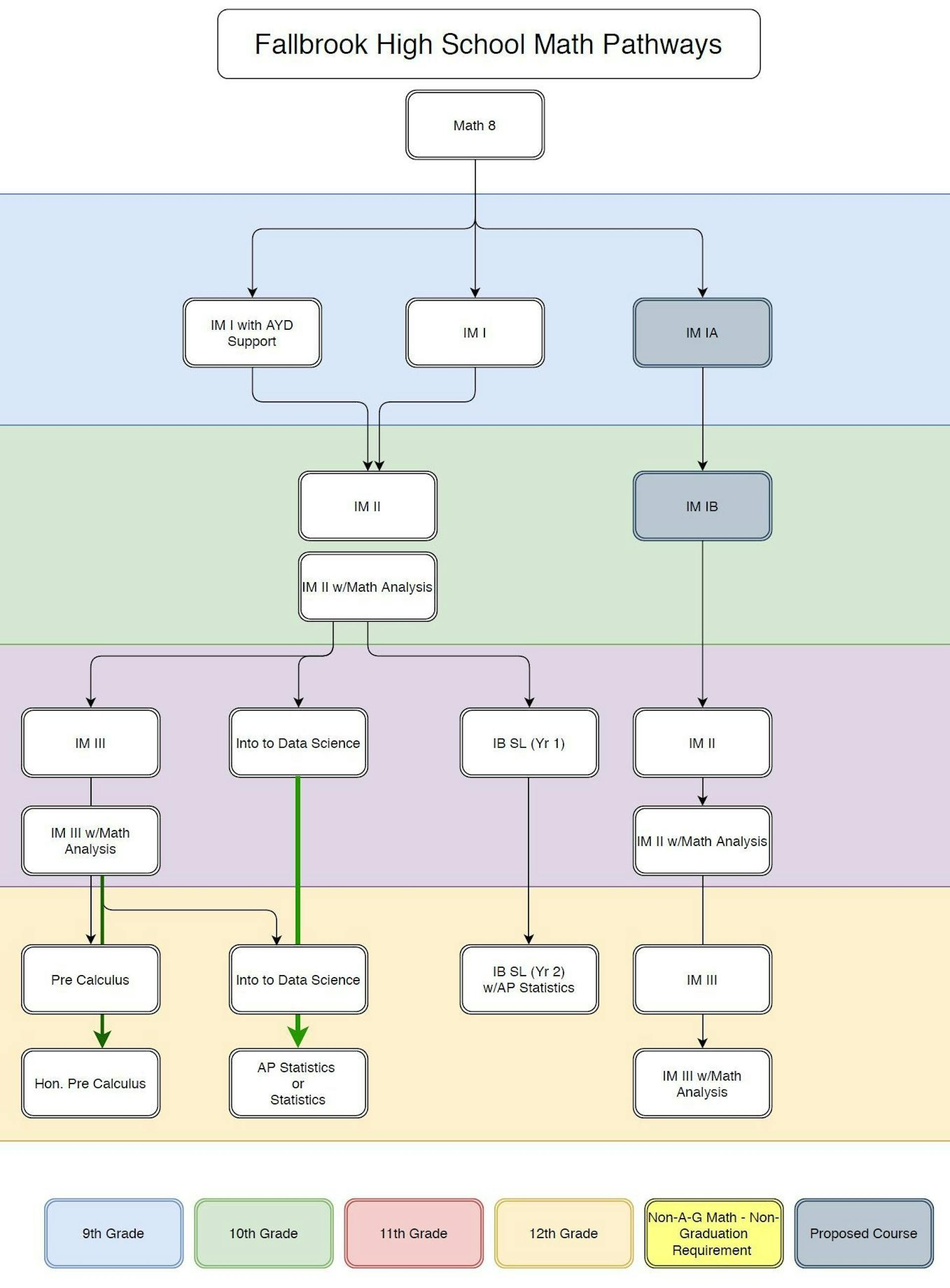
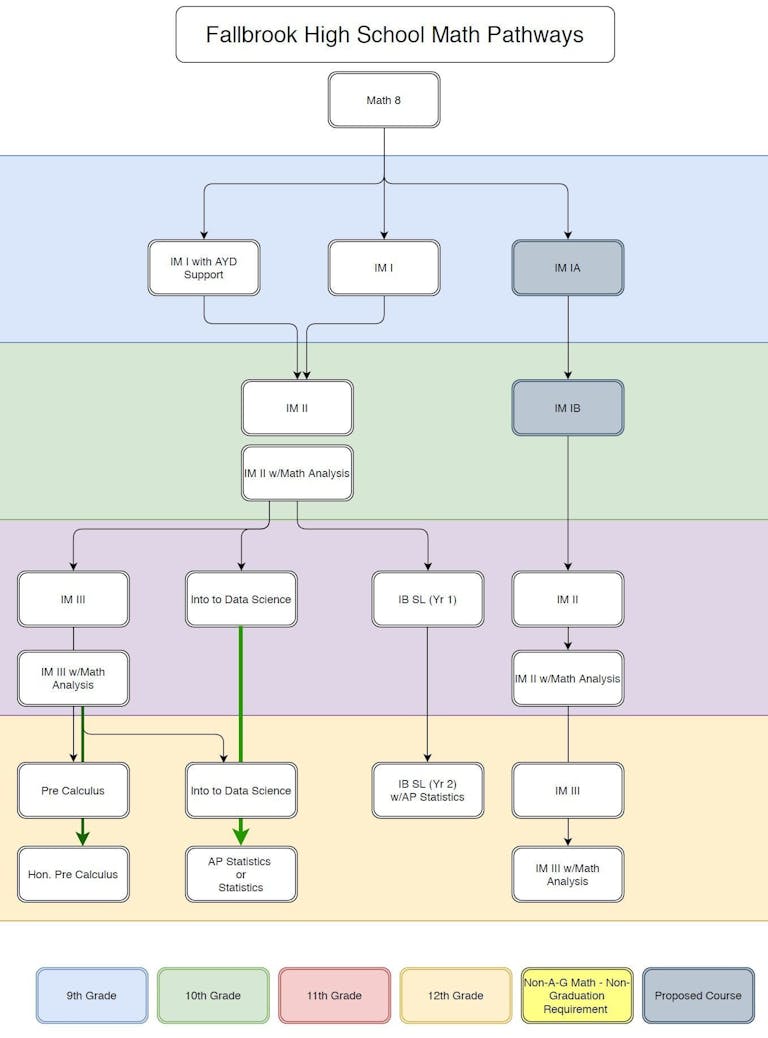
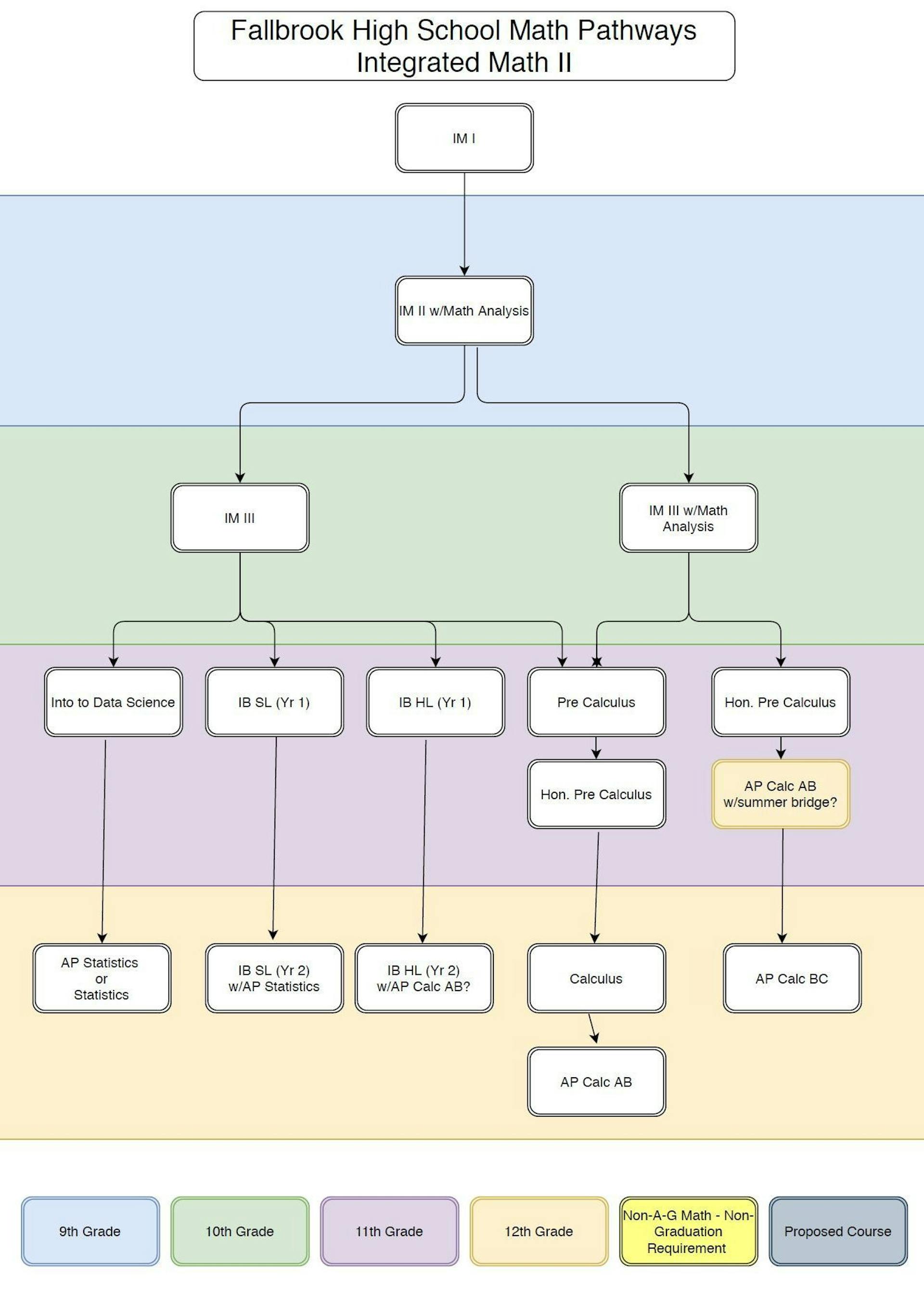
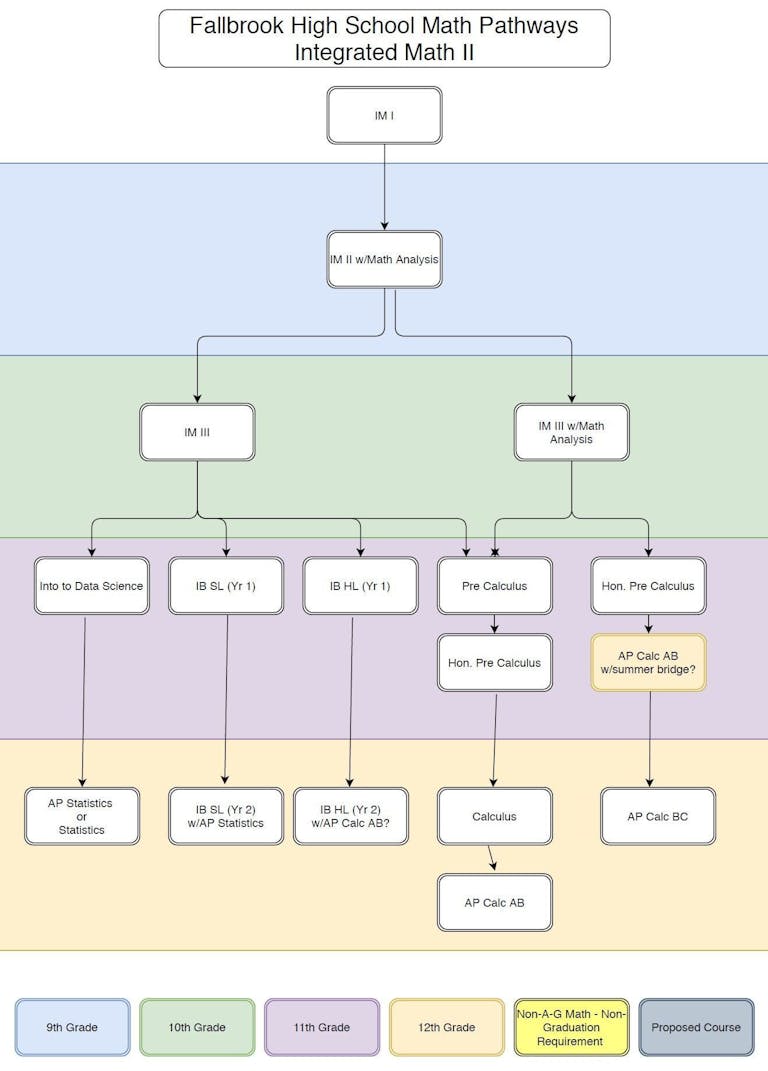
Courses
This is the first year-long course of a three –year high school mathematical sequence. Integrated Math 1 is
designed to combine some of the basic principles of Algebra 1, Geometry, and Statistics. Topics include Linear
and Exponential functions, Rigid Transformation and Constructions, Interpreting and Analyzing Univariate and
Bivariate data. The expectation is to develop and maintain a growth mindset for students and teach students
how to learn math in a collaborative process where multiple methods and representations are celebrated. The
Common Core Standards for Mathematical Practices will be addressed throughout the course.
Mathematics II is the second in a sequence of three integrated math courses. Successful completion of this course will
prepare students for the rigors of Integrated Math III. The focus of this course is on quadratic expressions, equations, andfunctions, comparing their characteristics and behavior to those of linear and exponential relationships from Mathematics I This course includes standards from the conceptual categories of Number and Quantity, Algebra, Functions, Geometry, and Statistics and Probability. For the Mathematics II course, instructional time should focus on five critical areas:
(1) extend the laws of exponents to rational exponents
(2) compare key characteristics of quadratic functions with those of linear and exponential functions
(3) create and solve equations and inequalities involving linear, exponential, and quadratic expressions
(4) extend work with probability
(5) establish criteria for similarity of triangles based on dilations and proportional reasoning.
Integrated Mathematics 2 with Math Analysis is the second course, in a sequence of three, that exposes
students to the rigor and depth of knowledge that is required in higher levels of mathematics such as AP
Calculus and IB math courses. The focus of the Mathematics II with Math Analysis course is on quadratic
expressions, equations, and functions, comparing their characteristics and behavior to those of linear and
exponential relationships from Mathematics I. In addition, this course introduces students to the topic of
Trigonometry and its applications. It includes standards from the conceptual categories of Number and
Quantity, Algebra, Functions, Geometry, and Statistics and Probability. Growth rates of functions will be
analyzed as well as characteristics such as end behavior, asymptotic behavior, and periodic behavior. For the
Mathematics II with Math Analysis course, instructional time should focus on six critical areas:
(1) extend the laws of exponents to rational exponents
(2) compare key characteristics of quadratic functions with those of linear and exponential functions
(3) create and solve equations and inequalities involving linear, exponential, quadratic, and trigonometric expressions
(4) extend work with probability
(5) establish criteria for similarity of triangles based on dilations and proportional reasoning. (6) extend similarity to trigonometry and the unit circle.
Integrated Mathematics 3 is the third course, in a sequence of three, that exposes students to the rigor and
depth of knowledge that is required in higher levels of mathematics such as AP Calculus and IB math courses.
For this course, instructional time will focus on the five key areas:
(1) deepen and extend understanding of the use of statistics with identifying different ways of collecting data and the conclusions that can be drawn
(2) apply operations to polynomial functions
(3) solve polynomial, rational, radical and trigonometric functions algebraically and graphically
(4) extend work with function families and the effects of transformations on them
(5) model and solve real world problems that require the use of polynomial, rational, radical, exponential, logarithmic, and trigonometric functions.
In Mathematics III with Math Analysis, students expand their repertoire of functions to include polynomial,
rational, and radical functions. They also expand their study of right triangle trigonometry to include general
triangles. And, additionally, students bring together all of their experience with functions and geometry to
create models and solve contextual problems. Finally, they will begin to explore calculus concepts such as
polar and parametric functions and vectors.
Introduction to Data Science (IDS) is designed to introduce students to the exciting opportunities available at
the intersection of data analysis, computing, and mathematics through hands-on activities. Data are
everywhere, and this curriculum will help prepare students to live in a world of data. The curriculum focuses
on practical applications of data analysis to give students concrete and applicable skills. Instead of using
small, tailored, curated data sets as in a traditional statistics curriculum, this curriculum engages students with
a wider world of data that fall into the "Big Data" paradigm and are relevant to students' lives. In contrast to
the traditional formula-based approach, in IDS statistical inference is taught algorithmically, using modern
randomization and simulation techniques. Students will learn to find and communicate meaning in data, and
to think critically about arguments based on data.
This course is designed for the advanced math student who is on track to take P Calculus the next school year,
as either a high school or college student. Applications, problem solving, reasoning, communication, and
technology will be integrated in preparation for calculus. Topics include linear, quadratic, and polynomial
functions, inequalities, graphs and inverses of functions, exponents and logarithms, conic sections,
trigonometric equations and applications, triangle trigonometry, trig addition, double and half-angle formulas,
polar and complex numbers, vectors and determinants, sequences and series, probability, limits, and
introduction to calculus.
This course of study is graphical, analytical, and numerical in nature. Calculus ties together seemingly
independent topics to create a “big picture” of mathematics. Topics include limits, continuity, differentiation
and its applications, integration, differentiation and integration of logarithmic, exponential, and other
transcendental functions, and area and volume found by integration principles. All topics that are found on
the AP Calculus AB exam are covered but, in less depth, and speed than the AP Calculus course.
AP Calculus AB is roughly equivalent to a first semester college calculus course devoted to topics in
differential and integral calculus. The AP course covers topics in these areas, including concepts and skills of
limits, derivatives, definite integrals, and the Fundamental Theorem of Calculus. The course teaches students
to approach calculus concepts and problems when they are represented graphically, numerically, analytically,
and verbally, and to make connections amongst these representations. Students learn how to use technology to
help solve problems, experiment, interpret results, and support conclusions. * This is a weighted course.
The IB Mathematics Applications and Interpretations SL is a two-year course containing topics including
descriptive and introductory inferential statistics; geometry and trigonometry; unit conversion; mathematical
models (linear, quadratic, exponential, and rational); introductory differential calculus; sets, probability, and
logic. The approach taken emphasizes the development of mathematical reasoning skills and the
understanding of fundamental concepts. Most topics are explored in a real-world context. Student’s design
and complete an independent data-based research project which also serves as the internal assessment portion
of their IB grade. Solid algebraic skills and the capacity for independent work are important to a student’s
success.
The IB Mathematics Applications and Interpretations SL is a two-year course containing topics including descriptive and introductory inferential statistics; geometry and trigonometry; unit conversion; mathematical models (linear, quadratic, exponential, and rational); introductory differential calculus; sets, probability, and logic. The approach taken emphasizes the development of mathematical reasoning skills and the understanding of fundamental concepts. Most topics are explored in a real-world context. Student’s design and complete an independent data-based research project which also serves as the internal assessment portion of their IB grade. Solid algebraic skills and the capacity for independent work are important to a student’s success. This course prepares students for the AP Statistics exam. This is a weighted course.
The IB Mathematics Applications and Interpretations HL (Part 1 and 2) is a two-year course containing
topics including descriptive and introductory inferential statistics; geometry and trigonometry; unit
conversion; mathematical models (linear, quadratic, exponential, and rational); introductory differential
calculus; sets, probability, and logic. The approach taken emphasizes the development of mathematical
reasoning skills and the understanding of fundamental concepts. Most topics are explored in a real-world
context. Student’s design and complete an independent data-based research project which also serves as the
internal assessment portion of their IB grade. Solid algebraic skills and the capacity for independent work are
important to a student’s success. * This is a weighted course.
The IB Mathematics Applications and Interpretations HL (Part 1 and 2) is a two-year course containing
topics including descriptive and introductory inferential statistics; geometry and trigonometry; unit
conversion; mathematical models (linear, quadratic, exponential, and rational); introductory differential
calculus; sets, probability, and logic. The approach taken emphasizes the development of mathematical
reasoning skills and the understanding of fundamental concepts. Most topics are explored in a real-world
context. Student’s design and complete an independent data-based research project which also serves as the
internal assessment portion of their IB grade. Solid algebraic skills and the capacity for independent work are
important to a student’s success. This course prepares students for the AP Calculus BC exam. * This is a
weighted course.
Resources


Khan Academy
We’re a nonprofit with the mission to provide a free, world-class education for anyone, anywhere.
Visit Page

